高校物理にとって、等速円運動の知識は、単振動、万有引力、波へと発展していく大事な概念です。
等速円運動の基礎知識を振り返りつつ、シュミレーションしたことを書いていきます。
教員や生徒で、シュミレーション に興味があったり、等速円運動をさらっと復習したい方向けの内容となりますが、高校物理からずいぶん遠ざかった大人の方も、この記事でなんとなく思い出してもらえたら嬉しいです!
等速円運動の基礎知識
等速円運動とは
等速円運動とは物体が一定の速さで円周上を動く運動のことです。
角速度とは
円運動をする物体が、単位時間あたりに回転する角度を角速度[rad/s]といいます。
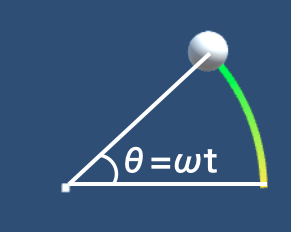
角度\( \theta {\rm [rad]}\)と角速度\( \omega{\rm [rad]}\)、時間\( t{\rm [s]}\)の間には、$$\theta= \omega t$$の関係があります。
1秒あたりの回転角である角速度ωに時間を掛けたら、どれだけ回転したかがでてくるってことですね。
速度について
等速円運動という名前がついているくらいなので、速さは一定ですが、速度は一定ではありません。
速さは大きさのみをもつスカラー量で、速度は向きと大きさをもつベクトル量だからです。速度の大きさ(速さ)は変わりませんが、向きは変わり続けます。
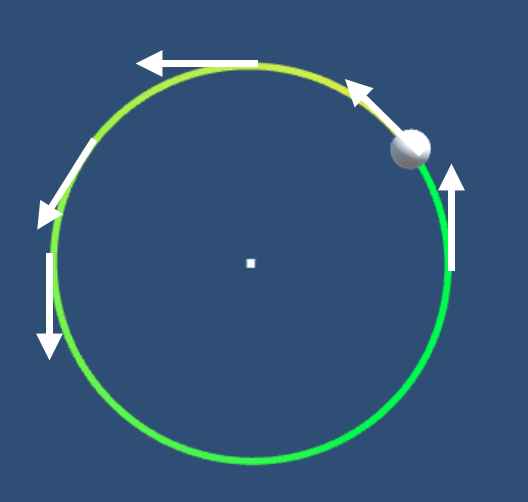
このように、速度の向きは常に円の接線方向となるので、向きは変わり続けます。
速度が変わり続けるということは、そこには加速度が生じているということです。
単位時間あたりの速度の変化
加速度について
等速円運動する物体には加速度が生じていると説明をしました。では向きについてはどうでしょうか。
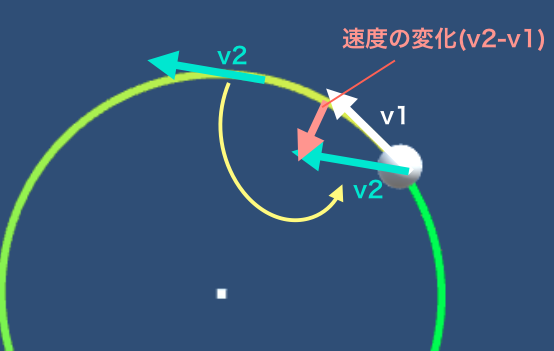
上の図のように、速度の変化を表すベクトルを作図することができ、円の中心方向を向くことがわかると思います。本当は瞬間の加速度まで書きたいけれど、今回は省略します…
そして、速度の変化の向きと加速度の向きは一致するので、加速度は円の中心方向を向きます。
導出はしませんが、加速度の大きさは角速度ω、半径rを用いて、$$a=r\omega ^2 $$となります。
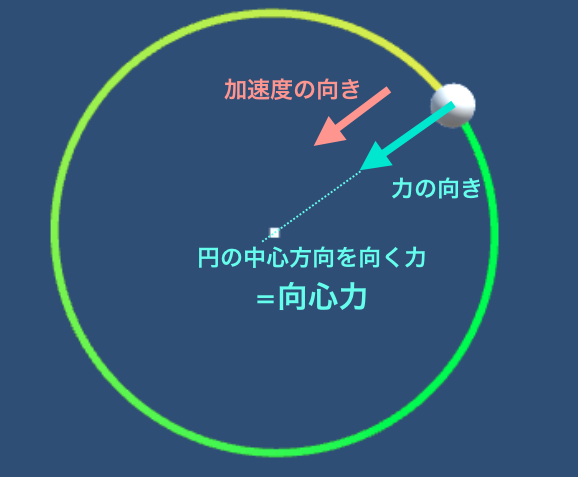
等速円運動する物体にはたらく力について
運動方程式$$m\overrightarrow{a} = \overrightarrow{F} $$より、加速度\( \overrightarrow{a}\)の向きと力\( \overrightarrow{F}\)の向きは一致することがわかります。そして、加速度の向きは円の中心方向を向くので、同じように力も円の中心方向を向きます。
この、円の中心方向を向く力のことを向心力といいます。
スクリプトを作成する
全体のコード
荒削りなところはありますが…
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class ConVelCircle : MonoBehaviour
{
public GameObject cube; //中心に配置するオブジェクトを取得
public float ome = 1.0f; //角速度ωの値
Rigidbody rb;
Transform myTransform;
Transform cubeTransform;
void Awake() //必要な情報を取得しておく
{
rb = this.GetComponent<Rigidbody>();
myTransform = this.transform;
cubeTransform = cube.transform;
}
private void Start()//初速を与える
{
//中心を原点としたときの物体の位置ベクトル
Vector3 dis = myTransform.position - cubeTransform.position;
//位置ベクトルの大きさ
float r = dis.magnitude;
//-------外積を計算-------(記事内で後述します)
Vector3 zDir = new Vector3(0.0f,0.0f,1.0f);
Vector3 perp = Vector3.Cross(zDir, dis);
Vector3 perpNor = perp.normalized;
//----------------------------
//初速v0=rω
float v_0 = r * ome;
rb.AddForce(v_0 *perpNor, ForceMode.VelocityChange);
}
void FixedUpdate() //向心力を与える
{
//物体から中心方向へのベクトル
Vector3 dis = cubeTransform.position - myTransform.position;
Vector3 rVec = dis.normalized;//正規化(大きさ1のベクトルにする)
float r = dis.magnitude; //半径
float m = rb.mass; //質量
//F=mrω^2
float force = m * r * ome * ome;
rb.AddForce(force*rVec);
}
}
いろいろ書いてあるけど、結局大事なところって、
//F=mrω^2
float force = m * r * ome * ome;ここだけですね!!
外積について
物体がどの位置にいても、円軌道を描く正しい初速を与えるために、外積を用いました。
外積とは、2つのベクトル
$$\overrightarrow{a}=
\left(
\begin{array}{c}
a_1 \\
a_2 \\
a_3\\
\end{array}
\right),
\overrightarrow{b}=
\left(
\begin{array}{c}
b_1 \\
b_2 \\
b_3\\
\end{array}
\right)
$$
に対して、
$$\overrightarrow{a} \times \overrightarrow{b}=
\left(
\begin{array}{c}
a_2 b_3-a_3b_2 \\
a_3b_1-a_1b_3 \\
a_1b_2 -a_2b_1\\
\end{array}
\right)
$$
の式で表せる値のことをいいます。
例えば、\( \overrightarrow{a}=(0,0,1) \)、\( \overrightarrow{b}=(2,0,0) \)の外積は\( \overrightarrow{a}\times \overrightarrow{b}=(0,2,0) \)となります。
今のことを図に表すと、
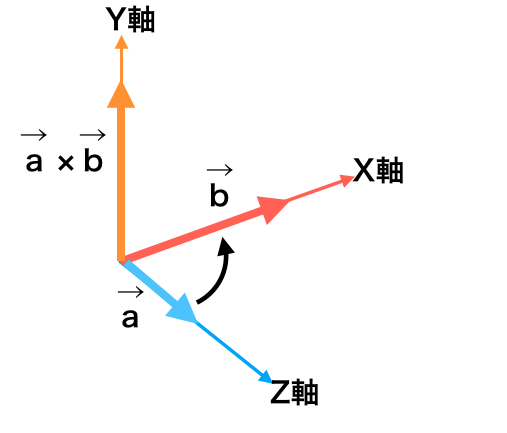
このように、すべてのベクトルは直交しています。\( \overrightarrow{a}\times \overrightarrow{b} \)の向きは、\( \overrightarrow{a}\)を\( \overrightarrow{b}\)の方向に回したときにネジが進む向きです(右ネジの法則)
外積の大きさは、\( \overrightarrow{a}\)と\( \overrightarrow{b}\)を2辺とする平行四辺形の面積に等しいという性質をもっています。
この性質を使って、初速の向きを指定しました。
今回は円の接線方向へ初速を与えたいので、

このようなベクトルの外積を計算することで、初速の向きを与えています。
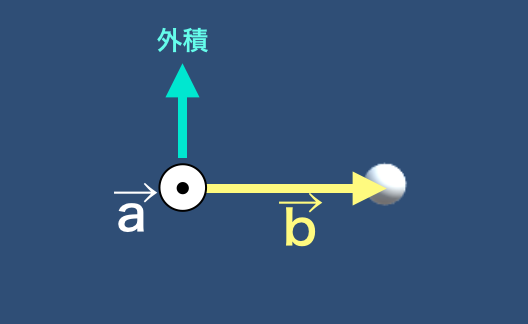
//中心を原点としたときの物体の位置ベクトル → bベクトル
Vector3 dis = myTransform.position - cubeTransform.position;
//-------外積を計算-------
Vector3 zDir = new Vector3(0.0f,0.0f,1.0f);//aベクトル
Vector3 perp = Vector3.Cross(zDir, dis);//外積を計算
Vector3 perpNor = perp.normalized;//正規化
//----------------------------このように向きを与えることで、物体を円軌道のどこから始めても正しい初速の向きを与えることができます。
以上です。ここまで読んでくださってありがとうございました。
また、物体の軌跡を描画する方法についてはこちらの記事を参考にさせていただきました。
この本読んで勉強中です。



コメント