物理基礎でも使える波の教材をUnityで作成していきたいと思います!
はじめの方に、波の基礎知識の説明、最後にUnityで使うスクリプトをのせます。
波とは
波は振動が伝わっていく現象です。それを伝える物質のことを媒質とよびます。ポイントは、
伝わるのは振動であり、媒質ではない
ということですね!どういうことかというと、次の動画を見てください。
波が伝わるようすを表した動画ですが、媒質の動きを見やすくしてみました。
波は右の方向に伝わっていますが、媒質は右に動くわけではなく、その場で振動しているだけですよね。
このように、波の伝わる方向と、媒質の動きが垂直なものを横波といいます。
波の式を導出する
原点(x=0)での媒質の振動を表す式
原点での媒質は単振動しています。単振動についてはこちらを
原点での変位(振動中心からのずれ)yを表す式は$$y=\sin \omega t$$です。ωは、等速円運動では角速度とよばれますが、単振動のときは角振動数とよばれます。
角振動数ωと周期Tには、$$\omega =\frac{2 \pi }{T} $$の関係があり、周期Tと振動数fの間には$$T=\frac{1}{f}$$の関係があるので、これを用いて変位yを表す式は$$y=\sin\frac{2 \pi }{T}t= \sin 2 \pi f t$$とかくことができます。
任意の位置xでの波の式
例えば、下の図で、ちょうど山となっている位置xでの波の式を考えていきたいと思います。
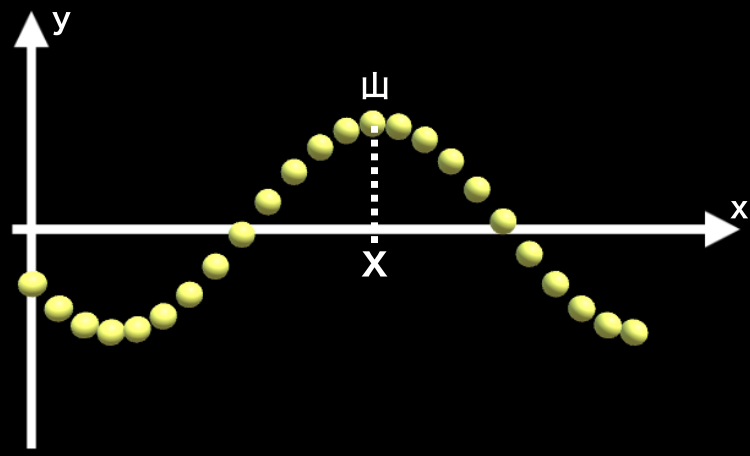
はじめにもいいましたが、波は振動が伝わっていく現象です。そして、この振動は、波源がどのように動くかで決まってくるので、言いかえれば、波とは波源の状態が伝わっていく現象です。
どういうことかというと…
今、「位置xではちょうど山となっているが、この山は波源から伝わってきたものだ」ということです。よく考えたら当たり前ですよね。
山が、波源から位置xに到達するまでの時間を\(t[{\rm s}]\)、波の伝わる速さを\(v[{\rm m/s}]\)、とすると、位置は$$x=vt$$と表すことができます。
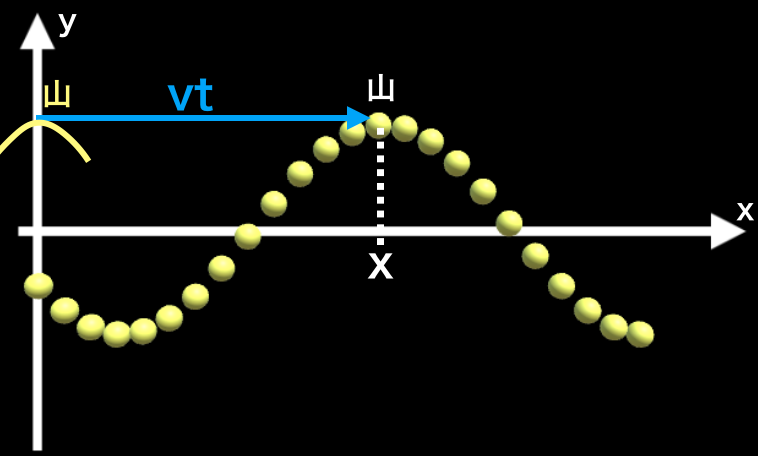
なので、山が波源から位置xに到達するまでの時間は$$t=\frac{x}{v}$$です。
この時間tをかけて山が到達したということは、逆にいうと、t秒前には山は原点にあったということです。
つまり、位置xでの媒質の状態は、t秒前の原点の状態と同じということです。
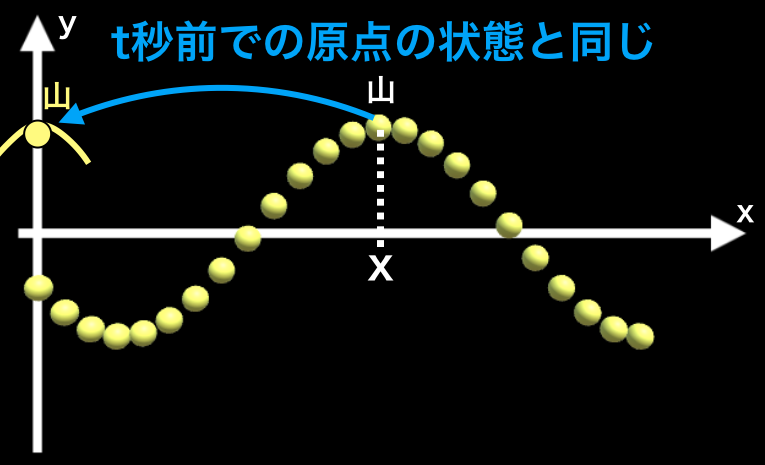
つまり任意の位置xでの変位を\(y_x(t)\)、原点x=0での変位を\(y_0(t)\)とおくと、$$y_x(t)=y_0(t-\frac{x}{v})$$となります。

これと、原点での振動の式をまとめると、
$$y_x(t)= \sin 2 \pi f\left( t-\frac{x}{v} \right)$$
となり、これが任意の位置xでの変位と、時間の関係式です。
Unityでの操作
C#スクリプト
今回用いたコードです。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class WaveControl : MonoBehaviour
{
public float amp = 4.0f; //振幅
public float fre = 0.25f;//振動数
public float spd = 5.0f; //速度
public float x_0 = 0.0f;//波源の位置
private float PI = Mathf.PI ;//πの値
private float x;//オブジェクト(媒質)のx座標
private float z;//オブジェクト(媒質)のz座標
private float Dis;//波源からの距離(変位)
Transform myTransform;
void Awake()
{
myTransform = this.transform;
}
void FixedUpdate()
{
Dis = x - x_0; //波源からの距離
x = myTransform.position.x;
z = myTransform.position.z;
//----------------------波の式 y=Asin2πf(t-x/v) ----------------------
float height = amp * Mathf.Sin(2.0f * PI * fre * (Time.time - (Dis / spd)));
//---------------------------------------------------------------
//-----------------はじめに波が到達するまで、媒質を静止させておく----------
if (Dis <= spd * Time.time)
{
myTransform.position = new Vector3(x, height, z);
}
else
{
myTransform.position = new Vector3(x, 0f, z);
}
//-----------------------------------------------------------------
}
}コード内の、「はじめに波が到達するまで、媒質を静止させておく」という部分を書かないと、スタートからすべての媒質が動いてしまいます。まぁ、これはこれでありだけど…
振動中心からの変位を意識させたいならば、各点の媒質を静止させた状態からスタートさせた方が効果ありです!
オブジェクトを複数配置する
GameObject → 3D Object → Sphere を作成し、先ほど作成したスクリプトをアタッチします。
また、ボールの色をみやすくするために、適当にMaterial を作成して、色を変えておきます。
作成したSphereを選択した状態で「command+d」ボタンを押すことで、オブジェクトを複製することができます。適当に4つくらい作っておきましょう。そして、それぞれのTransformのxを1ずつずらしておきます。(一番はじめのSphereのxは0です)
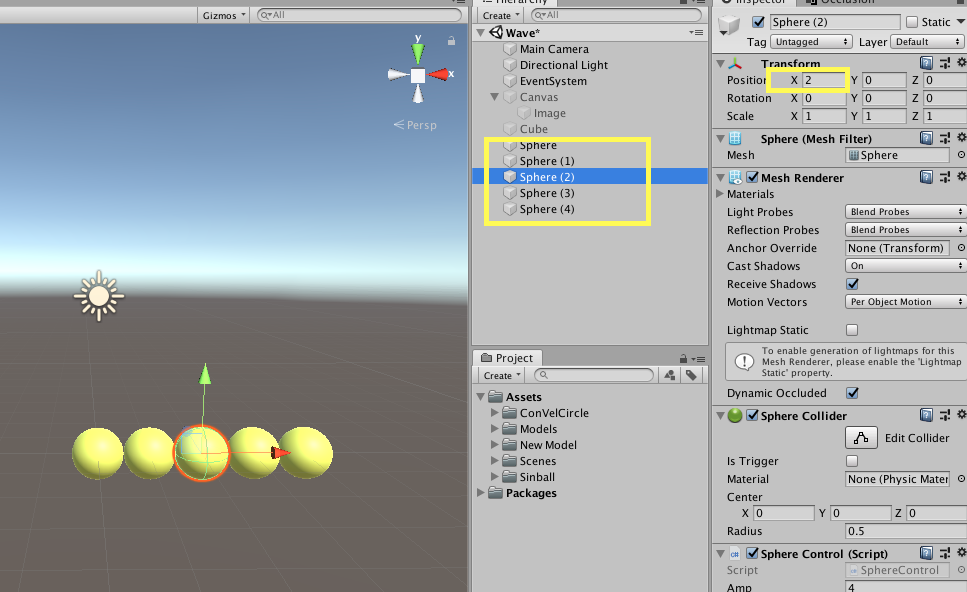
その後、Sphereを選択した状態で、「Sift」ボタンを押しながらSphere(4)を選択することで、作成したSphere達をすべて選択することができます。そして、「command+d」で複製しましょう。
複製されたオブジェクトを「command」ボタンを押しながら移動させます。そうすると、Transformをちょうど1ずつずらすことができます。
このようにして、20個くらい作成しておきます。
背景の画像を挿入する
GameObject → UI → Imageを作成します。
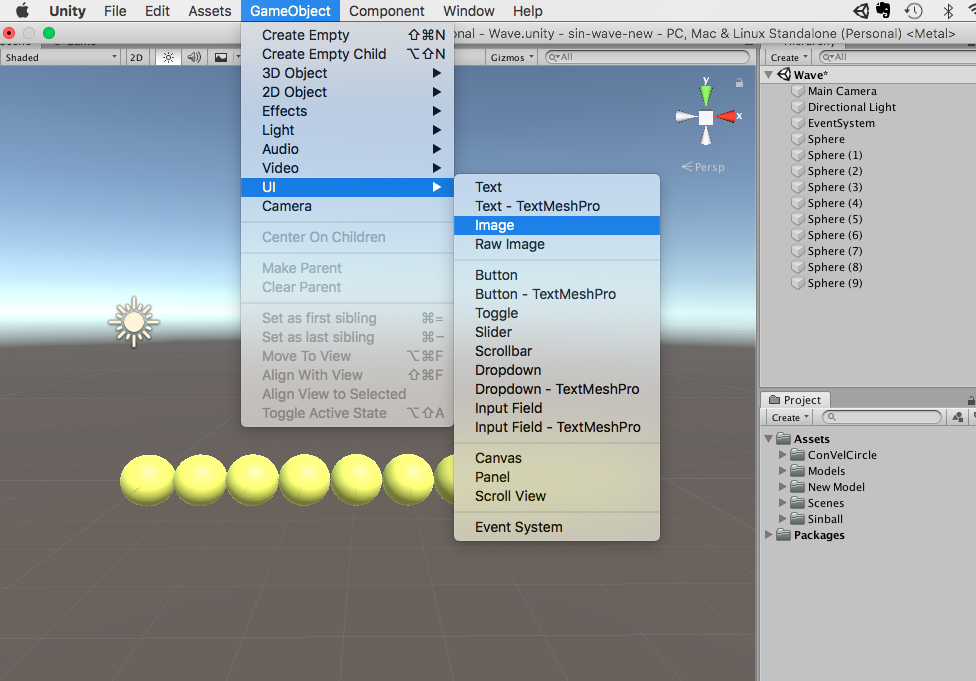
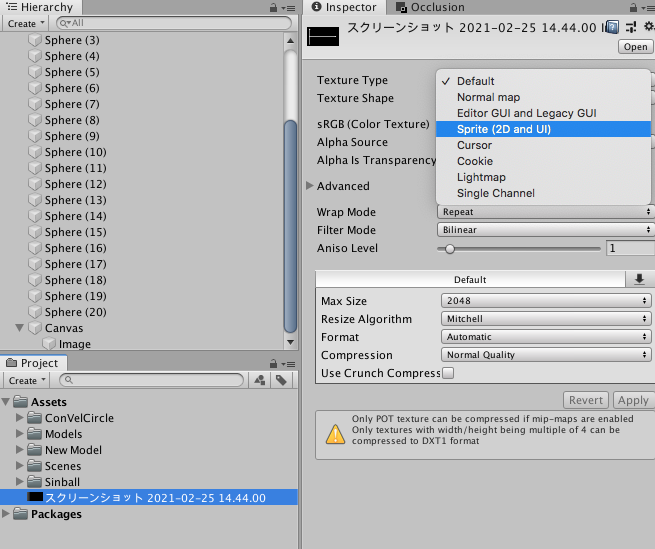
次に、挿入したい画像をProject内にドラックアンドドロップします。下の画像だと、「スクリーンショット2021…」っていうのですね。そして、Texture TypeというところがDefaultになっているので、Sprite(2D and UI)に変更します。確認画面が出てくるので、Applyを選択します。
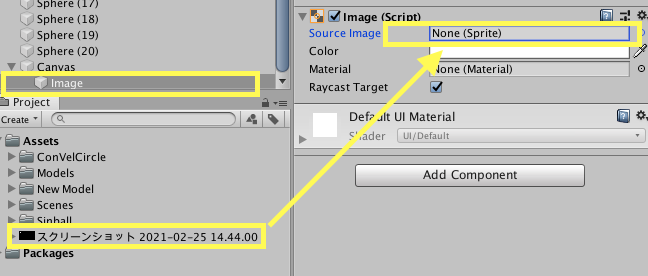
ImageのComponent内にある「Souce Image」に先程の画像を当てはめます。
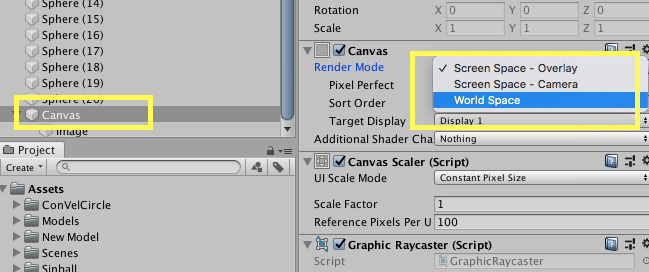
これで、Sceneに画像が表示されたと思いますが(結構変なとこにいるので探してみてください)、再生(Game)画面では、ボールの前に画像がきてしまうので、そこの設定をします。
Canvasを選択して、Componentの「Render mode」を見つけます。「Screen Space – Overlay」になっていますが、これを「World Space」に変更します。
あとは、Game画面などをみながら、Imageを好きな位置に配置していきます。ボールの前や後ろに好きに位置させることができます。
ImageのComponentであるRect Transform内をいろいろといじって、いい感じの位置にグラフを置きます。MainCamaeraの位置も大事です。
それでは終わります。ありがとうございました。
勉強させてもらってます!楽しい!




コメント