高校物理ではよく目にする、「ばねで連結された2物体に関する問題」について、シュミレーション してみました。最終的にはグラフを作成して理解を深めていきます!!
こちらの記事の続きになります
ばねで連結された2物体の運動
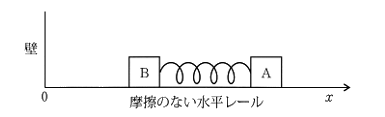
高校物理では、ばねにつながれた2物体に異なる初速を与えて運動させるという問題をよく目にします。問題を解く上では、2物体の重心は等速直線運動することを理解している必要があります。「運動量」という物理量を理解している人ならば、この物体系には外力がはたらかないため、「重心の運動量は変化しない」ことを理解できると思います。
生徒は机上では理解しながらも、実際にはどのような運動をするのかイメージできないことが多いです。そのため、実験を試みますが、ちょうどいい実験装置がない…
ということで、Unityを用いてシュミレーション していきます!
物体A、Bの位置を\(x_A\)、\(x_B\)と置くと、ばねの長さは\( (x_A-x_B)\)となります。また、ばねの自然長をLとすると、物体AとBにはたらく力\(F_A\)と\(F_B\)は$$\begin{eqnarray} F_A&=&-k(x_A-x_B-L)\\F_B&=&k(x_A-x_B-L)\end{eqnarray}$$と表せます。
また、2物体の重心xは、$$x=\frac{m_Ax_A+m_Bx_B}{m_A+m_B}$$とかけます。
これだけ知っていれば、シュミレーション することができます!
2物体を運動させるコード
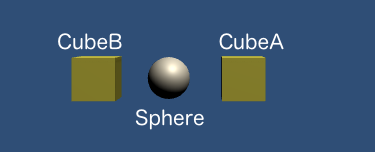
このようなオブジェクトを配置しました。SphereはCubeAとCubeBの重心位置を表しています。
SpringLinkというスクリプトを作成し(名前ださ!)、CubeAにアタッチします。
以下コードです
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class SprinkLink : MonoBehaviour
{
public GameObject cubeB;
public float springConstant = 2.0f; //ばね定数
public float v0A = 1.0f; //物体Aの初速
public float v0B = 3.0f; //物体Bの初速
private float naturalLength;
Rigidbody rbA;
Rigidbody rbB;
Transform cubeATransform;
Transform cubeBTransform;
void Awake()
{
rbA = this.GetComponent<Rigidbody>();
rbB = cubeB.GetComponent<Rigidbody>();
cubeATransform = this.transform;
cubeBTransform = cubeB.transform;
}
//2物体に弾性力を与える関数
void AddSpringForce(Vector3 cubeA_position, Vector3 cubeB_position, float k)
{
var dis = cubeA_position - cubeB_position; //2物体間の距離 (xA-xB)
var diff = dis - dis.normalized * naturalLength; //2物体間の距離-自然長 =ばねの伸び
var forceA = -1.0f * k * diff; //物体Aにはたらく力は-ばね定数*ばねの伸び=復元力
var forceB = 1.0f * k * diff; //物体Bにはたらく力はAにはたらく力の逆ベクトル
rbA.AddForce(forceA);
rbB.AddForce(forceB);
}
void Start()
{
var dis = cubeATransform.position - cubeBTransform.position; //初期状態での2物体間の距離
naturalLength = dis.magnitude;// 初期状態での2物体間の距離を自然長とする
Vector3 v_minus = new Vector3(-1.0f, 0.0f, 0.0f);
Vector3 v_pulus = new Vector3(1.0f, 0.0f, 0.0f);
rbA.AddForce(v0A * v_pulus, ForceMode.VelocityChange);
rbB.AddForce(v0B * v_pulus, ForceMode.VelocityChange);
}
void FixedUpdate()
{
AddSpringForce(cubeATransform.position, cubeBTransform.position, springConstant);
}
}
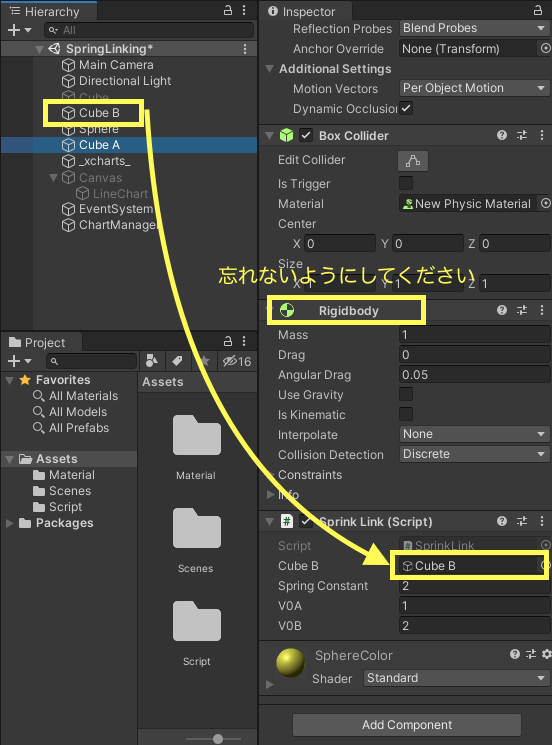
CubeA内に追加されたSpring Link(Script)にCubeBオブジェクトをアタッチします。また、CubeAとCubeBにRigidbodyコンポーネントを追加するのを忘れないようにしてください。
重心に置く物体のコード
次に、CubeAとCubeBの重心位置を表しているSphereオブジェクトにスクリプトをアタッチします。スクリプト名は「CenterGravity」としました。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class CenterGravity : MonoBehaviour
{
public GameObject cubeA;
public GameObject cubeB;
Rigidbody rbA;
Rigidbody rbB;
Transform cubeATransform;
Transform cubeBTransform;
void Awake()
{
rbA = cubeA.GetComponent<Rigidbody>();
rbB = cubeB.GetComponent<Rigidbody>();
cubeATransform = cubeA.transform;
cubeBTransform = cubeB.transform;
}
void FixedUpdate()
{
Vector3 xA = cubeATransform.position;
Vector3 xB = cubeBTransform.position;
float mA = rbA.mass;
float mB = rbB.mass;
Vector3 centerVec = (xA * mA + xB * mB) / (mA + mB);
this.transform.position = centerVec;
}
}
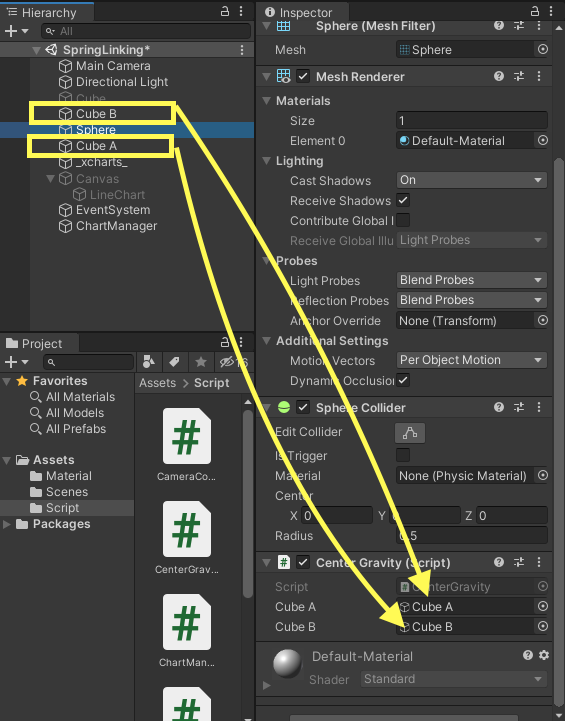
Sphereオブジェクトに追加されたCenter Gravityコンポーネント内にCubeA、CubeBオブジェクトをそれぞれアタッチします。
再生してみる
このように、2つの物体は単振動をしながら進んでいきます。また、物体の重心は等速直線運動していることが……わかりづらい….
よく見れば、等速直線運動な気もするけど、ちょっと微妙…ということで、グラフを描いて確かめていきます。
重心の運動を表すグラフを描く
グラフの描画については、こちらの記事で紹介しています。
ChartMangaerというグラフを描画するスクリプトを作成しました。
インスペクターから、y軸の最大値と最小値を変えられるようにしました。
public class ChartManager : MonoBehaviour
{
public float y_min = 0.0f;
public float y_max = 15f;
このように変更しておきます。
private void YAxisSet()
{
linechart.yAxes[0].type = Axis.AxisType.Value;
linechart.yAxes[0].minMaxType = Axis.AxisMinMaxType.Custom;
linechart.yAxes[0].min = y_min;
linechart.yAxes[0].max = y_max;
linechart.yAxes[0].splitNumber = 5;
}グラフの設定を次のようにしました。
再生してみます!
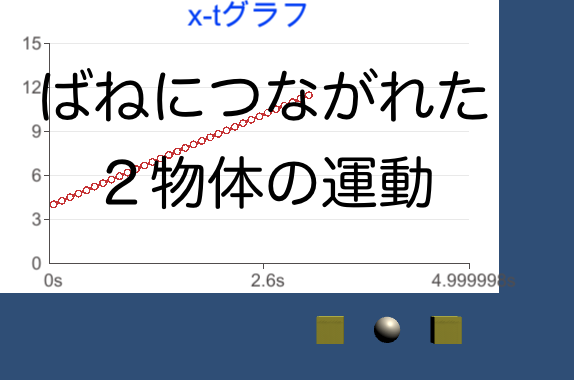
このように、x-tグラフが描かれます。
x-tグラフの傾き(\( \frac{dx}{dt}\))は速度を表しているので、
グラフが直線=傾きが一定=速度が一定
ということがわかります。



コメント